题目内容
已知曲线C1的参数方程为
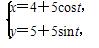 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
(1)将 消去参数t,化为普通方程(x-4)2+(y-5)2=25,
消去参数t,化为普通方程(x-4)2+(y-5)2=25,
即C1:x2+y2-8x-10y+16=0.
将 ,代入x2+y2-8x-10y+16=0得,
,代入x2+y2-8x-10y+16=0得,
ρ2-8ρcosθ-10ρsinθ+16=0.
所以C1的极坐标方程为
ρ2-8ρcosθ-10ρsinθ+16=0.
(2)C2的普通方程为x2+y2-2y=0.
 所以C1与C2交点的极坐标分别为(
所以C1与C2交点的极坐标分别为(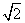 ,
,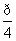 ),(2,
),(2, ).
).

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ,
, 对应的复数分别为z1,z2.
对应的复数分别为z1,z2.
 的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
 -
- =1 B.
=1 B.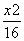 -
- =1
=1