题目内容
16．圆x2+（y-5）2=25的圆心到直线3x+4y-5=0的距离等于（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
分析 由圆的方程求出圆心坐标，再由点到直线的距离公式得答案．
解答 解：圆x2+（y-5）2=25的圆心坐标为（0，5），
由点到直线的距离公式可得圆心到直线3x+4y-5=0的距离等于$\frac{|4×5-5|}{\sqrt{{3}^{2}+{4}^{2}}}=3$．
故选：C．
点评 本题考查圆的标准方程，考查了点到直线的距离公式的应用，是基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
11．已知球O半径为$\sqrt{5}$，设S、A、B、C是球面上四个点，其中∠ABC=120°，AB=BC=2，平面SAC⊥平面ABC，则棱锥S-ABC的体积的最大值为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 3$\sqrt{3}$ |
1．直线3x+5y-7=0的斜率是（ ）
| A． | -$\frac{3}{5}$ | B． | -$\frac{5}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{3}{5}$ |
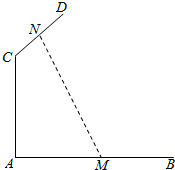如图，AB、CD为互相垂直的两异面直线，AC⊥AB，AC⊥CD，线段AC长为2，M∈AB，N∈CD，P为MN中点，且线段MN长为4，则点P的轨迹所形成的面积为（ ）