题目内容
若直线2ax+by-2=0（a，b∈R+）平分圆x2+y2-2x-4y-6=0，则
+
的最小值是（ ）
| 2 |
| a |
| 1 |
| b |
| A、1 | ||
| B、5 | ||
C、4
| ||
D、3+2
|
考点：直线与圆的位置关系
专题：不等式的解法及应用,直线与圆
分析：求出圆心，根据直线平分圆，得到直线过圆心，得到a，b的关系，利用基本不等式即可得到结论．
解答：
解：圆的标准方程为（x-1）2+（y-2）2=11，
即圆心为（1，2），
∵直线2ax+by-2=0（a，b∈R+）平分圆x2+y2-2x-4y-6=0，
∴直线过圆心，
即2a+2b-2=0，
∴a+b=1，
则
+
=（
+
）（a+b）=2+1+
+
≥3+2
=3+2
，
当且仅当
=
，即a=
b时取等号，
故
+
的最小值是3+2
，
故选：D．
即圆心为（1，2），
∵直线2ax+by-2=0（a，b∈R+）平分圆x2+y2-2x-4y-6=0，
∴直线过圆心，
即2a+2b-2=0，
∴a+b=1，
则
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| a |
| b |
|
| 2 |
当且仅当
| 2b |
| a |
| a |
| b |
| 2 |
故
| 2 |
| a |
| 1 |
| b |
| 2 |
故选：D．
点评：本题主要考查基本不等式的应用，利用直线和圆的位置关系得到a+b=1是解决本题的关键．
练习册系列答案
相关题目
执行如图的程序框图，那么输出S的值是（ ）
| A、2 | ||
B、
| ||
| C、-1 | ||
| D、1 |
若平面向量
，
的夹角为60°，且|
|=2|
|，则（ ）
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法正确的是（ ）
| A、命题“?x∈R使得x2+2x+3＜0”的否定是：“?x∈R，x2+2x+3＞0” | ||
B、a∈R，“
| ||
| C、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
D、命题p：“?x∈R，sinx+cosx≤
|
一个多面体的直观图和三视图所示，M是AB的中点，一只蝴蝶在几何体ADF-BCE内自由飞翔，由它飞入几何体F-AMCD内的概率为（ ）
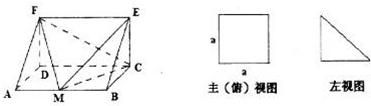
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若a=1且cosA=
，则△ABC的外接圆的直径等于（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|