题目内容
动点P向圆(x-1)2+y2=1引切线,使切线长总为2,则点P的轨迹方程为 .
考点:轨迹方程,圆的切线方程
专题:计算题,直线与圆
分析:由动点P向圆(x-1)2+y2=1引切线,使切线长总为2,可得圆心(1,0)与P的距离总为
,即可求出点P的轨迹方程.
| 5 |
解答:
解:∵动点P向圆(x-1)2+y2=1引切线,使切线长总为2,
∴圆心(1,0)与P的距离总为
,
∴点P的轨迹方程为(x-1)2+y2=5.
故答案为:(x-1)2+y2=5.
∴圆心(1,0)与P的距离总为
| 5 |
∴点P的轨迹方程为(x-1)2+y2=5.
故答案为:(x-1)2+y2=5.
点评:本题考查直线与圆的位置关系,考查圆的方程,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
sin410°+sin450°+sin470°=( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
“x<1”是“x2-3x+2>0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
两平行直线4x+3y-2=0与4x+3y+5=0之间的距离为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数(2+ai)(1-i)(a∈R)是纯虚数(是虚数单位),则a的值为( )
| A、-2 | B、-1 | C、2 | D、1 |
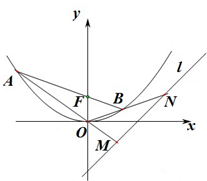 已知抛物线C的顶点为坐标原点O,焦点F(0,1)
已知抛物线C的顶点为坐标原点O,焦点F(0,1)