题目内容
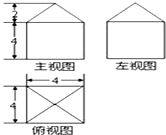
某几何体的三视图如图所示,计算该几何体的体积.

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个四棱柱与一个四棱锥组合而成的几何体,计算出底面面积和高,代入柱体和锥体体积公式,可得答案.
解答:
解:由已知的三视图可得:该几何体是一个四棱柱与一个四棱锥组合而成的几何体,
它们的底面面积均为4×4=16,
棱锥的高为2,故体积为:
×16×2=
,
棱柱的高为4,故体积为:4×16=64,
故组合体的体积V=
+64=
它们的底面面积均为4×4=16,
棱锥的高为2,故体积为:
| 1 |
| 3 |
| 32 |
| 3 |
棱柱的高为4,故体积为:4×16=64,
故组合体的体积V=
| 32 |
| 3 |
| 224 |
| 3 |
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
设
=2
-
+
,
=
+3
-2
,
=-2
+
-3
,
=3
+2
+5
,
,
,
是空间两两垂直的单位向量是否存在实数λμγ,使
=λ
+μ
+γ
成立?不存在请说明理由.
| a1 |
| i |
| j |
| k |
| a2 |
| j |
| j |
| k |
| a3 |
| i |
| j |
| k |
| a4 |
| i |
| j |
| k |
| i |
| j |
| k |
| a4 |
| a1 |
| a2 |
| a3 |
平面向量的集合A 到A的映射f(
)=
-2(
•
)
,其中
为常向量.若映射f满足f(
)•f(
)=
•
对任意的
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(-
|
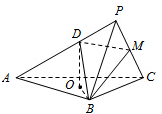 三棱锥P-ABC中,底面ABC为边长为2
三棱锥P-ABC中,底面ABC为边长为2