题目内容
16.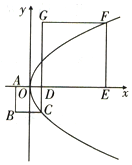 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |
分析 设正方形ABCD和正方形DEFG的边长分别为a,b(a<b),求出B,E的坐标,即可求出直线BE的斜率.
解答 解:设正方形ABCD和正方形DEFG的边长分别为a,b(a<b),
由题可得$C({\frac{a}{2},\;\;-a})$,$F({\frac{a}{2}+b,\;\;b})$,则$\left\{\begin{array}{l}{a^2}=pa,\;\;\\{b^2}=2p({\frac{a}{2}+b}),\;\;\end{array}\right.$
解得$a=p,\;\;b=(\sqrt{2}+1)p$,
则$B({-\frac{a}{2},\;\;-a})$,$E({\frac{a}{2}+b,\;\;0})$,
直线BE的斜率$k=\frac{0-(-a)}{{\frac{a}{2}+b-({-\frac{a}{2}})}}=\frac{a}{a+b}=\frac{p}{{(2+\sqrt{2})p}}=1-\frac{{\sqrt{2}}}{2}$,
故选B.
点评 本题考查抛物线的方程,考查直线斜率的计算,求出B,E的坐标是关键.

练习册系列答案
相关题目
11.设函数f(x)为定义域为R的奇函数,且f(x)=f(2-x),当x∈[0,1]时,f(x)=sinx,则函数g(x)=|cos(πx)|-f(x)在区间$[-\frac{5}{2},\frac{9}{2}]$上的所有零点的和为( )
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
6.将函数$y=sin(2x+\frac{π}{6})$的图象向左平移m(m>0)个单位长度,得到函数y=f(x)图象在区间$[-\frac{π}{12},\frac{5π}{12}]$上单调递减,则m的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
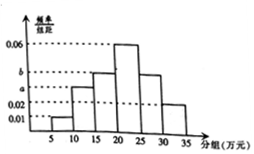 某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.
某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.