题目内容
1．
如图，有一个水平放置的透明无盖的正三棱柱容器，其中侧棱长为8cm，底面边长为12cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时，测得水深为6cm，如果不计容器的厚度，则球的表面积为（ ）| A． | 36πcm2 | B． | 64πcm2 | C． | 80πcm2 | D． | 100πcm2 |
分析 据图形的性质，求出截面圆的半径，即而求出求出球的半径，得出球的表面积．
解答 解：根据几何意义得出：边长为12的正三角形，球的截面圆为正三角形的内切圆（如图1），
∴内切圆的半径为O1D=2$\sqrt{3}$，
∵球面恰好接触水面时测得水深为6cm，
∴d=8-6-8=2，
∴球的半径为：R
R2=（R-2）2+（2$\sqrt{3}$）2，解得R=4
则球的表面积为4πR2=64π
故选：B
点评 本题考查了球的性质，解题的关键是求出球的半径，属于基础题．
练习册系列答案
相关题目
11．设函数f（x）为定义域为R的奇函数，且f（x）=f（2-x），当x∈[0，1]时，f（x）=sinx，则函数g（x）=|cos（πx）|-f（x）在区间$[-\frac{5}{2}，\frac{9}{2}]$上的所有零点的和为（ ）
| A． | 6 | B． | 7 | C． | 13 | D． | 14 |
12．下列命题中错误的是（ ）
| A． | 如果平面α外的直线a不平行于平面α，平面α内不存在与a平行的直线 | |
| B． | 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γ | |
| C． | 如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β | |
| D． | 一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交 |
16．三棱锥A-BCD内接于半径为2的球O，BC过球心O，当三棱锥A-BCD体积取得最大值时，三棱锥A-BCD的表面积为（ ）
| A． | $6+4\sqrt{3}$ | B． | $8+2\sqrt{3}$ | C． | $4+6\sqrt{3}$ | D． | $8+4\sqrt{3}$ |
6．将函数$y=sin（2x+\frac{π}{6}）$的图象向左平移m（m＞0）个单位长度，得到函数y=f（x）图象在区间$[-\frac{π}{12}，\frac{5π}{12}]$上单调递减，则m的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
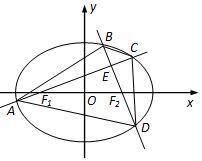已知椭圆W：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右两个焦点为F1，F2，且|F1F2|=2，椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$．
4．sin20°sin10°-cos10°sin70°=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |