题目内容
已知动圆C经过点(0,1),且在x轴截得的弦长为2,记该圆圆心的轨迹为E.
(1)求曲线E的方程;
(2)过点M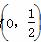 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为2
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为2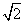 时,求直线m的方程.
时,求直线m的方程.
解析:(1)设圆C的圆心坐标为(x,y),则其半径r=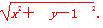 .
.
依题意,r2-y2=1,即x2+(y-1)2-y2=1,
整理得曲线E的方程为x2=2y.
(2)设A(x1,y1),B(x2,y2),则y1=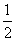 x
x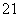 ,y2=
,y2=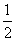 x
x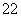 .
.
设直线m方程为y=kx+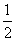 ,代入曲线E方程,得
,代入曲线E方程,得
x2-2kx-1=0,则x1+x2=2k.
对y=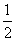 x2求导,得y′=
x2求导,得y′= x.
x.
于是过点A的切线为y=x1(x-x1)+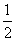 x
x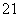 ,即y=x1x-
,即y=x1x-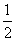 x
x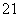 .①
.①
由①同理得过点B的切线为y=x2x-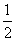 x
x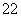 .②
.②
设C(x0,y0),由①、②及直线m方程得
x0=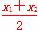 =k,y0=x1x0-
=k,y0=x1x0-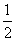 x
x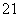 =-
=-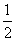 .
.
M为抛物线的焦点,y=-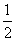 为抛物线的准线,由抛物线的定义,得
为抛物线的准线,由抛物线的定义,得
|AB|=y1+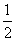 +y2+
+y2+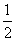 =k(x1+x2)+2=2(k2+1).
=k(x1+x2)+2=2(k2+1).
点C到直线m的距离d=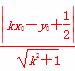 =
= .
.
所以△ABC的面积S=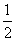 |AB|·d=(k2+1)
|AB|·d=(k2+1)  .
.
由已知(k2+1)  =2
=2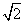 ,有且仅有k=±1.
,有且仅有k=±1.
故直线m的方程为y=±x+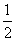 .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,则下列结论正确的是( )
,则下列结论正确的是( ) 是偶函数 (B)
是偶函数 (B) 上是增函数
上是增函数 
 -
- =1的焦点,PQ是过焦点F1的弦,那么|PF2|+|QF2|-
=1的焦点,PQ是过焦点F1的弦,那么|PF2|+|QF2|- |PQ|的值是__________.
|PQ|的值是__________.
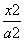 +
+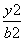 =1(a>
=1(a>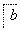 0)的离心率e=
0)的离心率e=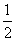 ,左焦点为F,A,B,
,左焦点为F,A,B, C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于( )
C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于( ) B.-3
B.-3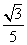 D.-
D.- P在曲线C2上,且直线l与椭圆C1有公共点,求椭圆C1的长轴长取得最小值时的椭圆方程.
P在曲线C2上,且直线l与椭圆C1有公共点,求椭圆C1的长轴长取得最小值时的椭圆方程. B.(x-1)2+(y-2)2=100
B.(x-1)2+(y-2)2=100 l被圆x2+y2-2y=0截得的弦长是( )
l被圆x2+y2-2y=0截得的弦长是( )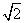 C.
C.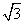 D.2
D.2