已知向量a1=.d=(1.1).对任意n∈N*都有an+1=an+d．(1)求|an|的最小值,(2)求正整数m.n.使am⊥an．题目和参考答案——青夏教育精英家教网—

题目内容

已知向量

=(1，-7)，

=(1，1)，对任意n∈N^*都有

an+1

．
（1）求|

|的最小值；
（2）求正整数m，n，使

⊥

．

考点：数列与向量的综合

专题：综合题,等差数列与等比数列,平面向量及应用

分析：（1）设

=（x_n，y_n），由

an+1

，可得{x_n}、{y_n}都是公差为1的等差数列，求出

=（n，n-8），即可求|

|的最小值；
（2）

⊥

等价于

•

=0，可得（m-4）（n-4）=-16，即可求出正整数m，n．

解答： 解：（1）设

=（x_n，y_n），由

an+1

得

xn+1=xn+1

yn+1=yn+1

∴{x_n}、{y_n}都是公差为1的等差数列…．（3分）
∵

=（1，-7），
∴x_n=n，y_n=n-8，
∴

=（n，n-8），
∴|

n2+(n-8)2

2(n-4)2+32

≥4

∴|

|的最小值为4

…..（6分）
（2）由（1）可设

=（m，m-8）

=（n，n-8）
由已知得：

•

=0
∴mn+（m-8）（n-8）=0
∴（m-4）（n-4）=-16…..（8分）
∵m，n∈N⁺
∴

m=2

n=12

或

m=3

n=20

或

m=12

n=2

或

m=20

n=3

…..（12分）

点评：本题考查数列与向量的综合，考查等差数列的通项，考查向量的数量积公式，属于中档题．

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

金榜夺冠真题卷系列答案

小升初综合素质检测卷系列答案

相关题目

已知平行四边形ABCD中，点E为CD的中点，

某四棱锥的三视图如图所示（单位：cm），则该四棱锥的体积是（　　）

cm³

a-a²（a∈R）．
（Ⅰ）若函数f（x）在区间（-∞，2）上单调递增，求实数a的取值范围；
（Ⅱ）记函数y=f（x）图象的顶点为P，A（0，2），O（0，0），当∠APO最大时，求实数a的值．

（理科学生做）已知点P₁（a₁，b₁），P₂（a₂，b₂），…，P_n（a_n，b_n），（n为正整数）都在函数y=(

)x的图象上．
（1）若数列{a_n}是等差数列，求证：数列{b_n}是等比数列；
（2）设an=n(n∈N*)，过点A_n（a_n+2，0），B_n（0，（n+2）b_n+1）的直线与两坐标轴所围成的三角形面积为c_n，试求最小的实数t，使c_n≤t对一切正整数n恒成立；
（3）对（2）中的数列{a_n}，对每个正整数k，在a_k与a_k+1之间插入3^k-1个3，得到一个新的数列{d_n}，设S_n是数列{d_n}的前n项和，试探究2014是否是数列{S_n}中的某一项，写出你探究得到的结论并给出证明．

已知f（x）是定义在R上的不恒为0的函数，且对于任意的a，b∈R，都满足f（ab）=af（b）+bf（a）．
（1）求f（0）、f（1）的值；
（2）判断f（x）的奇偶性，并证明你的结论；
（3）（文科）若f（2）=2，u_n=f（2ⁿ）（n∈N^*），求证：u_n+1＞u_n（n∈N^*）．
（3）（理科）若f（2）=2，u_n=

f(2-n)

(n∈N*)，求数列u_n的前n项和S_n．

在一条笔直的工艺流水线上有n个工作台，将工艺流水线用如图所示的数轴表示，各工作台的坐标分别为x₁，x₂，…，x_n，每个工作台上有若干名工人．现要在流水线上建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短．

（Ⅰ）若n=2，每个工作台上只有一名工人，试确定供应站的位置；
（Ⅱ）若n=5，工作台从左到右的人数依次为3，2，1，2，2，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值．

椭圆

=1（b＞0）的焦点在x轴上，左焦点为（-c，0），其右顶点关于直线x-y+4=0的对称点在直线x=-

上，
（1）求椭圆的方程；
（2）过椭圆的左焦点F的直线l交椭圆于A、B两点，交直线x=-

于点C，设O为坐标原点，且

，求△OAB的面积．

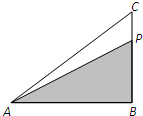如图，在Rt△ABC中，AB=4，BC=3，点P在边BC上沿B→C运动，则△ABP的面积小于4的概率为

．

试题分类