题目内容
在极坐标系中,直线l过点(1,0)且与直线θ=
(ρ∈R)垂直,则直线l极坐标方程为 .
| π |
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由条件利用用点斜式求直线的直角坐标方程,再把直角坐标方程化为极坐标方程.
解答:
解:直线θ=
(ρ∈R)的直角坐标方程为y=
x,故所求直线的斜率为-
,故所求直线的直角坐标方程为y-0=-
(x-1),
即
x+3y-
=0.
化为极坐标方程为
ρcosθ+3ρsinθ-
=0,即 ρcos(θ-
)=
,
故答案为:ρcos(θ-
)=
.
| π |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
即
| 3 |
| 3 |
化为极坐标方程为
| 3 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
故答案为:ρcos(θ-
| π |
| 3 |
| 1 |
| 2 |
点评:本题主要考查用点斜式求直线的直角坐标方程,把直角坐标方程化为极坐标方程的方法,属于基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积是( )
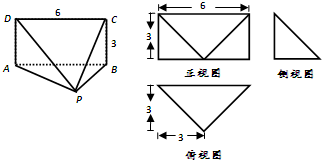

| A、54 | B、27 | C、18 | D、9 |
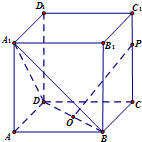 (理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
(理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
已知l,m为两条不同直线,α,β为两个不同平面,则下列命题中不正确的是( )
| A、若l∥α,m?α,则l∥m |
| B、若α∥β,l⊥α,则l⊥β |
| C、若α∥β,l?α,则l∥β |
| D、若α⊥β,α∩β=l,m?α,m⊥l,则m⊥β |