题目内容
已知离散型随机变量ξ1的概率分布为
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |
|
|
|
|
|
|
|
离散型随机变量ξ2的概率分布为
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |
|
|
|
|
|
|
|
求这两个随机变量数学期望、方差与标准差.
解:E(ξ1)=1×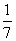 +2×
+2×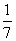 +…+7×
+…+7×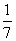 =4;
=4;
V(ξ1)=(1-4)2×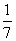 +(2-4)2×
+(2-4)2×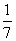 +…+(7-4)2×
+…+(7-4)2×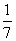 =4,σ1=
=4,σ1=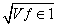 =2.
=2.
E(ξ2)=3.7×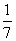 +3.8×
+3.8×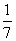 +…+4.3×
+…+4.3×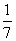 =4;
=4;
V(ξ2)=0.04,σ2= )=0.2.
)=0.2.

练习册系列答案
相关题目
甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η,且ξ、η分布列为
| ξ | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| η | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(1) 求a、b的值;
(2) 计算ξ、η的期望和方差,并以此分析甲、乙的技术状况.
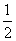 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是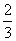 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.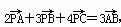 ,则△PAB与△PBC的面积的比值为__________.
,则△PAB与△PBC的面积的比值为__________.