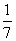题目内容
连续掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是________.

解析:由题意(m,n)·(-1,1)=-m+n<0,故m>n,基本事件总共有6×6=36个,符合要求的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),…,(5,4),(6,1),…,(6,5),共1+2+3+4+5=15个,故P= =
= .
.

练习册系列答案
相关题目
已知离散型随机变量ξ1的概率分布为
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |
|
|
|
|
|
|
|
离散型随机变量ξ2的概率分布为
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |
|
|
|
|
|
|
|
求这两个随机变量数学期望、方差与标准差.
下图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为________.
| 1 | 8 | 9 | |||
| 2 | 1 | 2 | 2 | 7 | 9 |
| 3 | 0 | 0 | 3 |
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1) 根据频数分布表计算苹果的重量在[90,95)的频率;
(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.