题目内容
甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是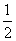 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是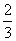 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.
(1) 分别求甲队以3∶0,3∶1,3∶2胜利的概率;
(2) 若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列.
解:(1) 记“甲队以3∶0胜利”为事件A1,“甲队以3∶1胜利”为事件A2,“甲队以3∶2胜利”为事件A3,由题意,各局比赛结果相互独立,故P(A1)=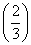
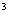 =
=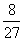 ,
,
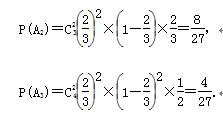 所以,甲队以3∶0、3∶1、3∶2胜利的概率分别是
所以,甲队以3∶0、3∶1、3∶2胜利的概率分别是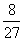 、
、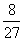 、
、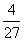 ;
;
(2) 设“乙队以3∶2胜利”为事件A4,由题意,各局比赛结果相互独立,
所以P(A4)=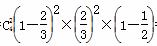 =
=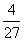 .
.
由题意,随机变量X的所有可能的取值为0,1,2,3,根据事件的互斥性得
P(X=0)=P(A1+A2)=P(A1)+P(A2)=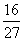 ,
,
P(X=1)=P(A3)=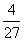 ,
,
P(X=2)=P(A4)=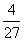 ,
,
P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=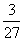 .
.
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P |
|
|
|
|

练习册系列答案
相关题目
已知离散型随机变量ξ1的概率分布为
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |
|
|
|
|
|
|
|
离散型随机变量ξ2的概率分布为
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |
|
|
|
|
|
|
|
求这两个随机变量数学期望、方差与标准差.
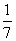
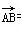 =2a+pb,
=2a+pb,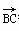 =a+b,
=a+b, =a-2b.若A、B、D三点共线,则实数p=________.
=a-2b.若A、B、D三点共线,则实数p=________.