题目内容
1. 如图,正方形ABCD与正方形ABEF边长均为1,且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动,若CM=BN=α(0<α<$\sqrt{2}$)
如图,正方形ABCD与正方形ABEF边长均为1,且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动,若CM=BN=α(0<α<$\sqrt{2}$)(1)求MN的长度;
(2)当α为何值时,MN的长最小.
分析 (1)过M作MP⊥AB,垂足为P,连接PN.运用平行线成比例可得PN∥AF,再由面面垂直的性质定理,可得AD⊥AF,根据勾股定理,我们易得MN2=MP2+PN2,可得MN的长度;
(2)由二次函数的性质,易得到MN的最小值.
解答 解: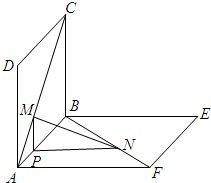 (1)过M作MP⊥AB,垂足为P,连接PN.
(1)过M作MP⊥AB,垂足为P,连接PN.
∵$\frac{AM}{MC}$=$\frac{AP}{PB}$,$\frac{AM}{MC}$=$\frac{FN}{NB}$,∴$\frac{AP}{PB}$=$\frac{FN}{NB}$,
∴PN∥AF,
平面ABCD⊥平面ABEF,AB⊥AD,
可得AD⊥平面BF,即有AD⊥AF,
即有∠MPN=90°MP=1-$\frac{\sqrt{2}}{2}$a,PN=$\frac{\sqrt{2}}{2}$a,
由勾股定理知:MN2=MP2+PN2=(1-$\frac{\sqrt{2}}{2}$a)2+($\frac{\sqrt{2}}{2}$a)2
=a2-$\sqrt{2}$a+1=(a-$\frac{\sqrt{2}}{2}$)2+$\frac{1}{2}$,
则MN=$\sqrt{{a}^{2}-\sqrt{2}a+1}$(0<a<$\sqrt{2}$);
(2)MN2=a2-$\sqrt{2}$a+1=(a-$\frac{\sqrt{2}}{2}$)2+$\frac{1}{2}$,
当a=$\frac{\sqrt{2}}{2}$时,MN取得最小值为$\frac{\sqrt{2}}{2}$.
点评 本题考查的知识点是空间中两点之间的距离运算,关键是将空间两点间的距离表示成a的函数,进而转化成求函数最值的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.函数$y=2sin(2x+\frac{π}{3})$的图象( )
| A. | 关于原点对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于y轴对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
16.如果已知sinα•cosα<0,sinα•tanα<0,那么角$\frac{α}{2}$的终边在( )
| A. | 第一或第二象限 | B. | 第一或第三象限 | C. | 第二或第四象限 | D. | 第四或第三象限 |
6.函数y=-cos2x+$\sqrt{3}$cosx+$\frac{5}{4}$,则( )
| A. | 最大值是$\frac{5}{4}$,最小值是1 | B. | 最大值是1,最小值是$\frac{1}{4}$-$\sqrt{3}$ | ||
| C. | 最大值是2,最小值是$\frac{1}{4}$-$\sqrt{3}$ | D. | 最大值是2,最小值是$\frac{5}{4}$ |