Question

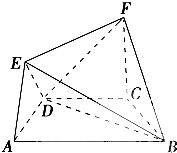在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF=1，
（1）求证：BD⊥平面AED；
（2）求B到平面FDC的距离．

Answer 1

考点：直线与平面垂直的判定,点、线、面间的距离计算

专题：空间位置关系与距离

分析：（1）由题意及图可得，先由条件证得AD⊥BD及AE⊥BD，再由线面垂直的判定定理即可证得线面垂直；
（2）设点B到平面FDC的距离为h，利用等积法即则V_F-CDB=V_B-FDC得到关于h的方程解之．

解答： （1）证明：∵四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，
∴∠ADC=∠BCD=120°．又CB=CD，
∴∠CDB=30°，
∴∠ADB=90°，AD⊥BD，
又AE⊥BD且，AE∩AD=A，AE，AD?平面AED，
∴BD⊥平面AED；
解：（2）设点B到平面FDC的距离为h，
则V_F-CDB=V_B-FDC，∴

1

3

S△CDBFC=

1

3

S△FDCh
∵S△CDB=

3

4

，S△CDB=

1

2

，
∴h=

3

2

．

点评：本题考查线面垂直的证明与点到面的距离的求法，解题的关键是熟练掌握线面垂直的判定定理及等积法求点到面的距离．