题目内容
下列选项叙述错误的是( )
| A、命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” |
| B、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| C、若命题p:?x∈R,x2+x十1≠0,则?p:?x∈R,x2+x+1=0 |
| D、若p∨q为真命题,则p,q均为真命题 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:由逆否命题的形式,即可判断A;运用充分必要条件的定义,即可判断B;
由命题的否定的形式,即可判断C;运用复合命题的真假和真值表,即可判断D.
由命题的否定的形式,即可判断C;运用复合命题的真假和真值表,即可判断D.
解答:
解:对于A.命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1”,则A对;
对于B.“x>2”可推出“x2-3x+2>0”,反之,不一定推出,则B对;
对于C.若命题p:?x∈R,x2+x十1≠0,则?p:?x∈R,x2+x+1=0,则C对;
对于D.若p∨q为真命题,则p,q中至少有一个为真,则D错.
故选D.
对于B.“x>2”可推出“x2-3x+2>0”,反之,不一定推出,则B对;
对于C.若命题p:?x∈R,x2+x十1≠0,则?p:?x∈R,x2+x+1=0,则C对;
对于D.若p∨q为真命题,则p,q中至少有一个为真,则D错.
故选D.
点评:本题考查简易逻辑的基础知识,考查四种命题的形式和充分必要条件的判断,及命题的否定和复合命题的真假,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知向量
=(-2,2,0),
=(1,0,-1),则它们的夹角是( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
如图:样本A和B分别取自两个不同的总体,他们的样本平均数分别为
A和
B,样本标准差分别为sA和sB,则( )
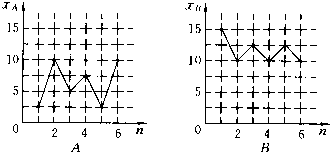
. |
| x |
. |
| x |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在分别标有号码2,3,4,…,10的9张卡片中,随机取出两张卡片,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若变量x,y满足约束条件
,则z=2x+3y的最小值为( )
|
| A、17 | B、14 | C、5 | D、3 |