题目内容
8.已知向量$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(1,m),若向量$\overrightarrow{a}$与2$\overrightarrow{a}$-$\overrightarrow{b}$共线,则m=$\frac{1}{3}$.分析 利用向量共线的充要条件,列出方程求解即可.
解答 解:向量$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(1,m),2$\overrightarrow{a}$-$\overrightarrow{b}$=(5,2-m)
向量$\overrightarrow{a}$与2$\overrightarrow{a}$-$\overrightarrow{b}$共线,
可得1×5=3×(2-m),解得m=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查向量的共线的充要条件的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设全集为R,集合A={x|y=lg(-x2+x)},B={x||x-1|≤1},则( )
| A. | (∁RA)∩B=∅ | B. | (∁RA)∩B=∁RA | C. | (∁RA)∩B=[1,2] | D. | (∁RA)∪B=R |
17.设Sn为数列{an}的前n项的和,且${S_n}=\frac{3}{2}({a_n}-1)(n∈{{N}^*})$,则an=( )
| A. | 3(3n-2n) | B. | 3n+2n | C. | 3n | D. | 3•2n-1 |
18.已知集合A={x∈Z|(x-2)(x-5)≤0},B={3,6},则下列结论成立的是( )
| A. | B⊆A | B. | A∪B=A | C. | A∩B=B | D. | A∩B={3} |
 如图所示,四棱椎P-ABCD中,底面ABCD为菱形,∠PBA=∠PBC
如图所示,四棱椎P-ABCD中,底面ABCD为菱形,∠PBA=∠PBC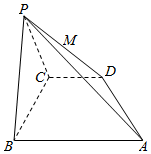 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.