题目内容
3.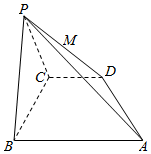 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.(1)平面α与四棱锥P-ABCD的面相交,交线围成一个梯形,在图中画出这个梯形;(不必说明画法及理由)
(2)求证:AB⊥平面PBC;
(3)若CD=1,求三棱锥M-ACD的体积.
分析 (1)取PC中点N,连结MN,AM,BN,则梯形MNBA即为要求的梯形;
(2)根据面面垂直的性质即可得出AB⊥平面PBC;
(3)作△PBC的中线PE,则M到底面的距离为$\frac{1}{2}PE$,代入体积公式计算.
解答  解:(1)取PC中点N,连结MN,AM,BN,则梯形MNBA为要求的梯形
解:(1)取PC中点N,连结MN,AM,BN,则梯形MNBA为要求的梯形
(2)∵∠ABC=90°,∴AB⊥BC.
∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB⊥BC,AB?平面ABCD,
∴AB⊥平面PBC.
(3)∵PB=PC=BC=2CD=2,∴△PBC是等边三角形,
过P作PE⊥BC,则PE⊥平面ABCD,且PE=$\sqrt{P{B}^{2}-B{E}^{2}}=\sqrt{3}$.
∴M到平面ACD的距离h=$\frac{1}{2}PE=\frac{\sqrt{3}}{2}$.
∵S△ACD=$\frac{1}{2}×CD×BC$=1.
∴三棱锥M-ACD的体积V=$\frac{1}{3}{S}_{△ACD}•h$=$\frac{1}{3}×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了平面的作法,面面垂直的性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
15.在△ABC中,a,b,c分别为内角A,B,C的对边,3cosA-cos(B+C)=1,a=$\sqrt{15}$,B=$\frac{π}{4}$,则b等于( )
| A. | $\sqrt{10}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
12.设集合M={x|log2(x-1)>0},集合N={x|x≥-2},则N∩∁RM=( )
| A. | {x|x≤-2} | B. | {x|-2<x≤2} | C. | {x|-2≤x≤3} | D. | {x|-2≤x≤2} |
13.若sin(θ-$\frac{π}{3}$)=$\frac{1}{3}$,0<θ<π,则cosθ=( )
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |