题目内容
16. 如图所示,四棱椎P-ABCD中,底面ABCD为菱形,∠PBA=∠PBC
如图所示,四棱椎P-ABCD中,底面ABCD为菱形,∠PBA=∠PBC(1)证明:PB⊥AC
(2)若PB=AB=2,∠ABC=∠PBD=60°,M为PB中点,求四面体M-ABC的体积.
分析 (1)设AC,BD交于点O,由△ABP≌△CBP得PA=PC,故PO⊥AC,又AC⊥BD,故而AC⊥平面PBD,得出PB⊥AC;
(2)过M作BD的垂线MN,则MN⊥平面ABCD,代入体积公式计算即可.
解答  证明:(1)连接AC、BD,设它们相交于点O,连接PO,则O为AC中点,
证明:(1)连接AC、BD,设它们相交于点O,连接PO,则O为AC中点,
∵AB=BC,∠PBA=∠PBC,PB=PB,
∴△ABP≌△CBP,∴PA=PC,
∴PO⊥AC,
∵底面ABCD为菱形,
∴AC⊥BD,又∵BD?平面PBD,PO?平面PBD,PO∩BD=O,
∴AC⊥平面PBD.∵PB?平面PBD,
∴PB⊥AC.
(2)∵底面ABCD为菱形,∠ABC=60°,
∴△ABC是等边三角形,AC=BC=2
∴${S_{△ABC}}=\frac{1}{2}×{2^2}sin{60°}=\sqrt{3}$.
过点M作MN⊥BD,垂足为N,
由(1)知NM⊥AC,故MN⊥平面ABCD,
在Rt△MBN中,$MN=MBsin{60°}=\frac{{\sqrt{3}}}{2}$,
四面体M-ABC的体积$V=\frac{1}{3}{S_{△ABC}}×MN=\frac{1}{3}×\sqrt{3}×\frac{{\sqrt{3}}}{2}=\frac{1}{2}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
4.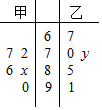 一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
 一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
6.执行如图所示的程序框图,则输出的结果是( )
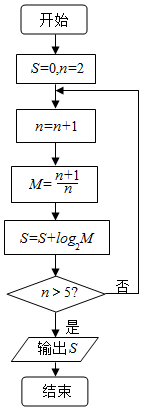

| A. | 1 | B. | log2$\frac{6}{5}$ | C. | log2$\frac{7}{3}$ | D. | log23 |