题目内容
18.已知集合A={x∈Z|(x-2)(x-5)≤0},B={3,6},则下列结论成立的是( )| A. | B⊆A | B. | A∪B=A | C. | A∩B=B | D. | A∩B={3} |
分析 由(x-2)(x-5)≤0,解得2≤x≤5,又x∈Z,可得集合A={2,3,4,5},利用集合的运算性质即可判断出结论.
解答 解:∵(x-2)(x-5)≤0,
解得2≤x≤5,又x∈Z,
∴集合A={2,3,4,5},B={3,6},
∴A∩B={3},
故选:D.
点评 本题考查了一元二次不等式的解法、集合的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,则输出的结果是( )
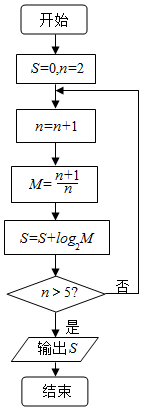

| A. | 1 | B. | log2$\frac{6}{5}$ | C. | log2$\frac{7}{3}$ | D. | log23 |
13.若sin(θ-$\frac{π}{3}$)=$\frac{1}{3}$,0<θ<π,则cosθ=( )
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |
3.在公差不为0的等差数列{an}中,a2+a4=ap+aq,记$\frac{1}{p}$+$\frac{9}{q}$的最小值为m,若数列{bn}满足b1=$\frac{2}{11}$m,2bn+1-bn•bn+1=1,则b1+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{10{0}^{2}}$=( )
| A. | $\frac{97}{100}$ | B. | $\frac{99}{100}$ | C. | $\frac{100}{101}$ | D. | $\frac{102}{101}$ |