题目内容
12.设全集为R,集合A={x|y=lg(-x2+x)},B={x||x-1|≤1},则( )| A. | (∁RA)∩B=∅ | B. | (∁RA)∩B=∁RA | C. | (∁RA)∩B=[1,2] | D. | (∁RA)∪B=R |
分析 解不等式-x2+x>0便可得出A=(0,1),而解不等式|x-1|≤1便可得出B=[0,2],然后进行补集、交集和并集的运算,从而找出正确选项.
解答 解:解-x2+x>0得,0<x<1;
∴A=(0,1);
解|x-1|≤1得,0≤x≤2;
∴B=[0,2];
∴∁RA=(-∞,0]∪[1,+∞);
∴(∁RA)∩B=[1,2]∪{0},(∁RA)∪B=R.
故选:D.
点评 考查描述法表示集合,以及补集、交集和并集的运算,一元二次不等式的解法,绝对值不等式的解法.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
3.下列不等式中成立的是( )
| A. | sin140°<sin30° | B. | cos140°<cos130° | C. | tan40°<tan30° | D. | sin40°<sin30° |
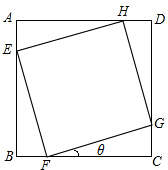 如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).
如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).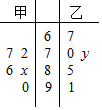 一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )