题目内容
已知(
-
)n的展开式中,前三项系数的绝对值依次成等差数列.
(1)求展开式中的常数项;
(2)求展开式中所有整式项.
| x |
| 1 | ||
2
|
(1)求展开式中的常数项;
(2)求展开式中所有整式项.
考点:二项式定理
专题:二项式定理
分析:(1)先求出二项式展开式的通项公式,再根据前三项系数的绝对值依次成等差数列,求出n的值.再令通项公式中x的幂指数为0,求得k的值,即可求得展开式中的常数项.
(2)要使Tk+1为整式项,需x的幂指数4-k为非负数,结合0≤k≤8,求得k的值,可得展开式中的整式项.
(2)要使Tk+1为整式项,需x的幂指数4-k为非负数,结合0≤k≤8,求得k的值,可得展开式中的整式项.
解答:
解:(1)由于二项式的展开式的通项公式为 Tr+1=C
•(
)n-r•(
)r•(-1)r,
∴前三项系数的绝对值分别为C
,
C
,
C
,
由题意知C
=C
+
C
,∴n=1+
n(n-1),n∈N*,解得n=8或n=1(舍去),
∴Tk+1=C
•(
)8-k•(-
)k=C
•(-
)k•x4-k,0≤k≤8.
令4-k=0,求得k=4,∴展开式中的常数项为T5=C
(-
)4=
.
(2)要使Tk+1为整式项,需4-k为非负数,且0≤k≤8,∴k=0,1,2,3,4.
∴展开式中的整式项为:x4,-4x3,7x2,-7x,
.
r n |
| x |
| 1 | ||
2
|
∴前三项系数的绝对值分别为C
0 n |
| 1 |
| 2 |
1 n |
| 1 |
| 4 |
2 n |
由题意知C
1 n |
0 n |
| 1 |
| 4 |
2 n |
| 1 |
| 8 |
∴Tk+1=C
k 8 |
| x |
| 1 | ||
2
|
k 8 |
| 1 |
| 2 |
令4-k=0,求得k=4,∴展开式中的常数项为T5=C
4 8 |
| 1 |
| 2 |
| 35 |
| 8 |
(2)要使Tk+1为整式项,需4-k为非负数,且0≤k≤8,∴k=0,1,2,3,4.
∴展开式中的整式项为:x4,-4x3,7x2,-7x,
| 35 |
| 8 |
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若F(
)=x,则下列等式正确的是( )
| 1-x |
| 1+x |
| A、F(2-x)=1-F(x) | ||
B、F(-x)=
| ||
| C、F(x-1)=F(x) | ||
| D、F(F(x))=-x |
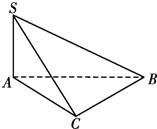 已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.
已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.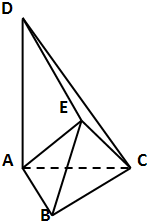 如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2
如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2