题目内容
x2+ax+1≤0对x∈[-1,1]恒成立,求a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:直接由二次不等式对应的二次函数开口向上得到不等式组
,解此不等式组得答案.
|
解答:
解:∵x2+ax+1≤0对应的二次函数y=x2+ax+1开口向上,
要使x2+ax+1≤0对x∈[-1,1]恒成立,
则
,此不等式组无解.
∴使x2+ax+1≤0对x∈[-1,1]恒成立的a的值不存在.
要使x2+ax+1≤0对x∈[-1,1]恒成立,
则
|
∴使x2+ax+1≤0对x∈[-1,1]恒成立的a的值不存在.
点评:本题考查了函数恒成立问题,考查了利用“三个二次”的结合求解参数问题,体现了数学转化思想方法,是中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
在△ABC中,∠A,∠B,∠C所对的边为a,b,c,a=8,B=60°,A=45°,则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|
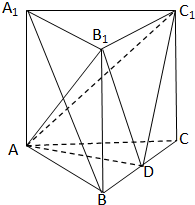 如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点