题目内容

若（1+ex）2014=a0+a1x+a2x2+…+a2014x2014（x∈R），则-
a1
e
+
a2
e2
-…+
a2014
e2014
（　　）
A、eB、1C、-1D、-e
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，令x=-
1
e
，可得a0-
a1
e
+
a2
e2
-…+
a2014
e2014
=0．再令x=0求得a0 的值，从而求得-
a1
e
+
a2
e2
-…+
a2014
e2014
的值．
解答： 解：在（1+ex）2014=a0+a1x+a2x2+…+a2014x2014（x∈R）中，令x=-
1
e
，
可得a0-
a1
e
+
a2
e2
-…+
a2014
e2014
=0．
再令x=0可得a0=1，∴-
a1
e
+
a2
e2
-…+
a2014
e2014
=-1，
故选：C．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于中档题．
练习册系列答案
相关题目
已知集合M={f（x）|f2（a）-f2（b）=f（a+b）•f（a-b），x，y∈R}，有下列命题：
①若f1（x）=
1，  x≥0
-1，x＜0
，则f1（x）∈M；
②若f2（x）=2x，则f2（x）∈M；
③若f3（x）∈M，则y=f3（x）的图象关于原点对称；
④若f4（x）∈M，则对于任意不等的实数x1，x2，总有
f4(x1)-f4(x2)
x1-x2
＜0成立．
其中所有正确命题的序号是（　　）
A、①③B、①④C、②③D、②④
不等式log2（-x2+x+2）＞1的解集为（　　）
A、（-2，0）
B、（-1，1）
C、（0，1）
D、（1，2）
数列{an}中，an+1=
an2
2an-5
，已知该数列既是等差数列又是等比数列，则该数列的前20项的和等于（　　）
A、100
B、0或100
C、100或-100
D、0或-100
定义由如图框图表示的运算，若f（x）=|x+1|+|x-1|，则输出y=（　　）
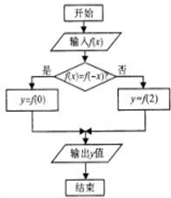
A、0B、1C、2D、4
已知函数f（x）=alnx+
1
2
bx2-（b+a）x．
（Ⅰ）当a=1，b=0时，求f（x）的最大值；
（Ⅱ）当b=1时，设α，β是f（x）两个极值点，且α＜β，β∈（1，e]（其中e为自然对数的底数）．求证：对任意的x1，x2∈[α，β]，|f（x1）-f（x2）|＜1．
已知函数f（x）=
1
3
x3+
1-a
2
x2-ax-a，x∈R，其中a＞0．
（1）求函数f（x）的单调区间；
（2）若函数f（x）在区间（-3，0）内恰有两个零点，求a的取值范围；
（3）当a=1时，设函数f（x）在区间[t，t+3]上的最大值为M（t），最小值为m（t），记g（t）=M（t）-m（t），求函数g（t）在区间[-4，-1]上的最小值．
设数列{an}，a1=1，an+1=
an
3
+
1
3n
．数列{bn}，bn=3n-1an．正数数列{dn}，dn2=1+
1
bn2
+
1
bn+12
．
（1）求证：数列{bn}为等差数列；
（2）设数列{bn}，{dn}的前n项和分别为Bn，Dn，求数列{bnDn+dnBn-bndn}的前n项和Sn．
已知数列{an}满足a1=1，|an+1-an|=pn，n∈N*．
（Ⅰ）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；
（Ⅱ）若p=
1
2
，且{a2n-1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网