题目内容
已知函数f(x)=alnx+
bx2-(b+a)x.
(Ⅰ)当a=1,b=0时,求f(x)的最大值;
(Ⅱ)当b=1时,设α,β是f(x)两个极值点,且α<β,β∈(1,e](其中e为自然对数的底数).求证:对任意的x1,x2∈[α,β],|f(x1)-f(x2)|<1.
| 1 |
| 2 |
(Ⅰ)当a=1,b=0时,求f(x)的最大值;
(Ⅱ)当b=1时,设α,β是f(x)两个极值点,且α<β,β∈(1,e](其中e为自然对数的底数).求证:对任意的x1,x2∈[α,β],|f(x1)-f(x2)|<1.
考点:实际问题中导数的意义,函数恒成立问题
专题:证明题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求出当a=1,b=0时的函数f(x)的表达式,求出导数,以及单调区间,从而判断极值,注意这里也是最值;
(Ⅱ)写出b=1时的函数f(x)的表达式,并求出导数,由条件得到α=1,β=a,说明x1,x2∈[α,β]是减区间,从而|f(x1)-f(x2)|≤f(1)-f(a),化简并令g(x)=
(x2-1)-xlnx(1<x≤e),通过求导,判断g(x)在(1,e]内是增,从而g(x)≤
(e2-1)-elne即
(a2-1)-alna≤
,而
<1,故结论成立.
(Ⅱ)写出b=1时的函数f(x)的表达式,并求出导数,由条件得到α=1,β=a,说明x1,x2∈[α,β]是减区间,从而|f(x1)-f(x2)|≤f(1)-f(a),化简并令g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| e2-1-2e |
| 2 |
| e2-1-2e |
| 2 |
解答:
(Ⅰ)解:当a=1,b=0时,f(x)=lnx-x(x>0),
导数f′(x)=
-1,当x>1时,f′(x)<0,
当0<x<1时,f′(x)>0,
∴x=1时,函数取极大值,也为最大值,且为-1;
(Ⅱ)证明:当b=1时,f(x)=alnx+
x2-(1+a)x,
导数f′(x)=
+x-(1+a)=
(x>0),
∵α,β是f(x)两个极值点,且α<β,β∈(1,e],
∴α=1,β=a,(1<a≤e),
∴当1<x<a时,f′(x)<0,即函数f(x)递减,
当x>a或0<x<1,f′(x)>0,即函数f(x)递增,
∵任意的x1,x2∈[α,β],则函数f(x)在该区间内是减函数,
∴f(1)最大且为
-(1+a),f(a)最小且为alna+
a2-(1+a)a,
∴|f(x1)-f(x2)|≤f(1)-f(a)=
-(1+a)-alna-
a2+(1+a)a
=
(a2-1)-alna,
令g(x)=
(x2-1)-xlnx(1<x≤e)
则g′(x)=x-1-lnx,g′(1)=0,g′(e)=e-1-1>0,
∴g(x)在(1,e]上递增,
故g(x)≤
(e2-1)-elne=
,即
(a2-1)-alna≤
,
而
<1,
∴|f(x1)-f(x2)|<1.
导数f′(x)=
| 1 |
| x |
当0<x<1时,f′(x)>0,
∴x=1时,函数取极大值,也为最大值,且为-1;
(Ⅱ)证明:当b=1时,f(x)=alnx+
| 1 |
| 2 |
导数f′(x)=
| a |
| x |
| (x-1)(x-a) |
| x |
∵α,β是f(x)两个极值点,且α<β,β∈(1,e],
∴α=1,β=a,(1<a≤e),
∴当1<x<a时,f′(x)<0,即函数f(x)递减,
当x>a或0<x<1,f′(x)>0,即函数f(x)递增,
∵任意的x1,x2∈[α,β],则函数f(x)在该区间内是减函数,
∴f(1)最大且为
| 1 |
| 2 |
| 1 |
| 2 |
∴|f(x1)-f(x2)|≤f(1)-f(a)=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
令g(x)=
| 1 |
| 2 |
则g′(x)=x-1-lnx,g′(1)=0,g′(e)=e-1-1>0,
∴g(x)在(1,e]上递增,
故g(x)≤
| 1 |
| 2 |
| e2-1-2e |
| 2 |
| 1 |
| 2 |
| e2-1-2e |
| 2 |
而
| e2-1-2e |
| 2 |
∴|f(x1)-f(x2)|<1.
点评:本题主要考查导数在函数中的综合运用:求单调区间和求极值、最值,同时考查函数在一区间内的任两个函数值的差的绝对值不大于最大值与最小值的差,考查运用函数的单调性比较大小,是一道综合题.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为5,则|AB|等于( )
| A、12 | B、8 | C、6 | D、4 |
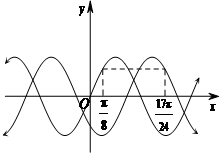 已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )
已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )
一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )A、4π+
| ||||
B、4π+
| ||||
C、2π+
| ||||
D、2π+
|