题目内容
数列{an}中，an+1=
，已知该数列既是等差数列又是等比数列，则该数列的前20项的和等于（ ）
| an2 |
| 2an-5 |
| A、100 |
| B、0或100 |
| C、100或-100 |
| D、0或-100 |
考点：数列递推式,数列的求和
专题：点列、递归数列与数学归纳法
分析：由数列{an}既是等差数列又是等比数列，可知数列是不等于0的常数列，设出数列的项后代入已知数列递推式得答案．
解答：
解：∵数列{an}既是等差数列又是等比数列，
∴数列是不等于0的常数列，
则设an+1=an=a（a≠0）．
代入an+1=
，得：
a=
，
即a2-5a=0．
解得：a=5．
∴数列的前20项的和等于20a=100．
故选：A．
∴数列是不等于0的常数列，
则设an+1=an=a（a≠0）．
代入an+1=
| an2 |
| 2an-5 |
a=
| a2 |
| 2a-5 |
即a2-5a=0．
解得：a=5．
∴数列的前20项的和等于20a=100．
故选：A．
点评：本题考查了数列递推式，解答此题需注意的是，既是等差数列又是等比数列的数列只有非零常数列，是中低档题．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
“a＞m＞1”是“logam＜1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
对任意的实数k，直线y=kx+1与圆x2+y2=2的位置关系是（ ）
| A、相离 | B、相切 |
| C、相交 | D、随k的变化而变化 |
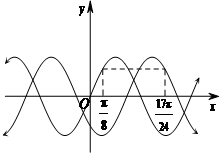已知函数y=g（x）的图象由f（x）=sin2x的图象向右平移φ（0＜φ＜x）个单位得到，这两个函数的部分图象如图所示，则φ=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在等差数列{an}中，若a2=4，a5=13，则a6=（ ）
| A、14 | B、15 | C、16 | D、17 |
一个几何体是由圆柱和正三棱锥组合而成，其正视图和俯视图如图所示，则该几何体的表面积是（ ）A、4π+
| ||||
B、4π+
| ||||
C、2π+
| ||||
D、2π+
|
如图所示，四边形PDCE为矩形，四边形ABCD为直角梯形，且∠BAD=∠ADC=90°，平面PDCE⊥平面ABCD，AB=AD=