题目内容
不等式log2（-x2+x+2）＞1的解集为（ ）
| A、（-2，0） |
| B、（-1，1） |
| C、（0，1） |
| D、（1，2） |
考点：指、对数不等式的解法
专题：函数的性质及应用
分析：根据对数函数的定义域及单调性，将不等式log2（-x2+x+2）＞1，等价变形为-x2+x+2＞2，再用一元二次不等式求解即可得到答案．
解答：
解：∵log2（-x2+x+2）＞1
∴-x2+x+2＞2
解得0＜x＜1
故选：C
∴-x2+x+2＞2
解得0＜x＜1
故选：C
点评：本题主要考查对数不等式的解法，求解本题的关键是正确应用对数函数的单调性，解题时要注意函数的定义域．，这是本题中的一个易错点，忘记定义域的限制出错．
练习册系列答案
相关题目
已知i是虚数单位，m∈R，且
是纯虚数，则（
）2008等于（ ）
| 2-mi |
| 1+i |
| 2-mi |
| 2+mi |
| A、1 | B、-1 | C、i | D、-i |
已知两点A（-1，5），B（3，9），则线段AB的中点坐标为（ ）
| A、（1，7） |
| B、（2，2） |
| C、（-2，-2） |
| D、（2，14） |
对任意的实数k，直线y=kx+1与圆x2+y2=2的位置关系是（ ）
| A、相离 | B、相切 |
| C、相交 | D、随k的变化而变化 |
双曲线2y2-x2=4的虚轴长是（ ）
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
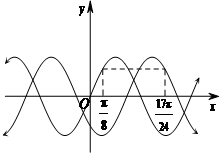已知函数y=g（x）的图象由f（x）=sin2x的图象向右平移φ（0＜φ＜x）个单位得到，这两个函数的部分图象如图所示，则φ=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在等差数列{an}中，若a2=4，a5=13，则a6=（ ）
| A、14 | B、15 | C、16 | D、17 |