题目内容
6.若抛物线y2=2x上的一点到其准线的距离为2,则该点的坐标可以是( )| A. | $({\frac{1}{2}\;\;,\;\;1})$ | B. | $({1\;\;,\;\;\sqrt{2}})$ | C. | $({\frac{3}{2}\;\;,\;\;\sqrt{3}})$ | D. | (2,2) |
分析 根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得x的值,代入抛物线方程求得y值,即可得到所求点的坐标.
解答 解:∵抛物线方程为y2=2x,
∴焦点为F($\frac{1}{2}$,0),准线为l:x=-$\frac{1}{2}$,
∵抛物线y2=2x上一点到其准线的距离为2,
即x+$\frac{1}{2}$=2,解之得x=$\frac{3}{2}$,
代入抛物线方程求得y=±$\sqrt{3}$,
∴点的坐标为:($\frac{3}{2}$,$±\sqrt{3}$).
故选:C.
点评 本题主要考查了抛物线的简单性质.在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
1.函数f(x)=ln(x2-1)的定义域为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,1)∪(1,+∞) | C. | (1,+∞) | D. | (0,1) |
18.若集合A={-2,0,1,3},B={-1,1,3}则A∪B元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |


 如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.
如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.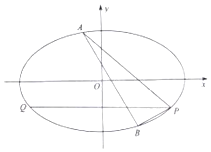 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)