题目内容
17．函数f（x）=log2x+1与g（x）=2-x-1在同一平面直角坐标系下的图象大致是（ ）| A． |  | B． |  | C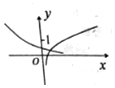． |  | D． |  |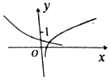
分析 根据函数f（x）=1+log2x与g（x）=2-x-1解析式，分析他们与同底的指数函数、对数函数的图象之间的关系，（即如何变换得到），分析其经过的特殊点，即可用排除法得到答案．
解答 解：∵f（x）=1+log2x的图象是由y=log2x的图象上移1而得，
∴其图象必过点（1，1）．
故排除A、B，
又∵g（x）=2-x-1=2-（x+1）的图象是由y=2-x的图象左移1而得，
故其图象也必过（-1，1）点，及（0，$\frac{1}{2}$）点，
故排除C，
故选D．
点评 本题主要考查对数函数和指数函数图象的平移问题，属于容易题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图是遂宁市某校高二年级20名学生某次体育考试成绩（单位：分）的频率分布直方图：
8．已知结合M={y|y=sinx，x∈N}，N={-1，0，1}，则M∩N是（ ）
| A． | {-1，0，1} | B． | {0，1} | C． | {0} | D． | {1} |
5．
某校高三年级在学期末进行的质量检测中，考生数学成绩情况如下表所示：
已知用分层抽样方法在不低于135分的考生中随机抽取5名考生进行质量分析，其中文科考生抽取了1名．
（1）求z的值；
（2）如图是文科不低于135分的6名学生的数学成绩的茎叶图，计算这6名考生的数学成绩的方差；
（3）已知该校数学成绩不低于120分的文科理科考生人数之比为1：3，不低于105分的文科理科考生人数之比为2：5，求理科数学及格人数．
某校高三年级在学期末进行的质量检测中，考生数学成绩情况如下表所示：| 数学成绩 | [90，105） | [105，120） | [120，135） | [135，150] |
| 文科考生 | 57 | 40 | 24 | 6 |
| 理科考生 | 123 | x | y | z |
（1）求z的值；
（2）如图是文科不低于135分的6名学生的数学成绩的茎叶图，计算这6名考生的数学成绩的方差；
（3）已知该校数学成绩不低于120分的文科理科考生人数之比为1：3，不低于105分的文科理科考生人数之比为2：5，求理科数学及格人数．
2．函数y=log3（x2-2x+4）的值域为（ ）
| A． | [1，+∞） | B． | [0，+∞） | C． | [3，+∞） | D． | R |
9．直线y=kx+1（k∈R）与椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$恒有两个公共点，则m的取值范围为（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | （1，5）∪（5，+∞） | D． | [1，5）∪（5，+∞） |
6．若抛物线y2=2x上的一点到其准线的距离为2，则该点的坐标可以是（ ）
| A． | $（{\frac{1}{2}\;\;，\;\;1}）$ | B． | $（{1\;\;，\;\;\sqrt{2}}）$ | C． | $（{\frac{3}{2}\;\;，\;\;\sqrt{3}}）$ | D． | （2，2） |