题目内容
12. 已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.
已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.(1)求f(f(2))的值
(2)画出此函数的图象.
(3)若f(x)=2,求x的值.
分析 根据分段函数的解析式,即可求出f(f(2)),画出图象即可,由图象得到结论.
解答  解:(1):f(2)=$\frac{1}{2}$×2=1,f(1)=1,
解:(1):f(2)=$\frac{1}{2}$×2=1,f(1)=1,
∴f(f(2))=1,
(2)如图所示,
(3)当由图象可知,x2=2,解得x=$\sqrt{2}$,或$\frac{1}{2}$x=2,解得x=4.
故f(x)=2事,x的值为$\sqrt{2}$,4
点评 本题考查了函数图象和画法和函数图象的识别,以及函数值的求法,属于基础题.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
20.命题P:“A=30°”是命题Q:“sinA=$\frac{1}{2}$”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
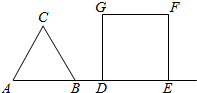 如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.
如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.