题目内容
2．如图，半径为4的球O中有一内接圆往，则圆柱的侧面积最大值是32π．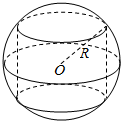
分析 设出圆柱的上底面半径为r，球的半径与上底面夹角为α，求出圆柱的侧面积表达式，求出最大值
解答 解：∵设圆柱的上底面半径为r，球的半径与上底面夹角为α，则r=4cosα，圆柱的高为8sinα，
∴圆柱的侧面积为：32πsin2α，当且仅当α=$\frac{π}{4}$时，sin2α=1，圆柱的侧面积最大，
∴圆柱的侧面积的最大值为：32π．
故答案为：32π．
点评 本题是基础题，考查球的内接圆柱的知识，圆柱的侧面积的最大值的求法，考查计算能力，常考题型．
练习册系列答案
优生乐园系列答案
相关题目
已知函数$f（x）=\left\{\begin{array}{l}x+2{\;}^{\;}（x＜0）\\{x^2}{\;}^{\;}{\;}^{\;}（0≤x＜2）\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}（x≥2）\end{array}\right.$．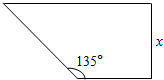
某植物园要建形状为直角梯形的苗圃（如图所示），两条邻边借用夹角为135°的两面墙，另两条边的总长为60m，设垂直于底边的腰长为x（m）．
14．${∫}_{1}^{2}$（x+2x）dx等于（ ）
| A． | （x+2x）|${\;}_{1}^{2}$ | B． | （x2+2xln2）|${\;}_{1}^{2}$ | ||
| C． | （$\frac{{x}^{2}}{2}$+2x）|${\;}_{1}^{2}$ | D． | （$\frac{{x}^{2}}{2}$+$\frac{{2}^{x}}{ln2}$）|${\;}_{1}^{2}$ |