题目内容
17.若函数y=f(x)满足f(x+2)=f(x),且x∈[-1,1]时,$f(x)=cos\frac{πx}{2}$,函数$g(x)=\left\{\begin{array}{l}lgx,x>0\\-\frac{1}{x},x<0\end{array}\right.$,则函数h(x)=f(x)-g(x)在区间[-5,5]内零点的个数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 由f(x+2)=f(x),得函数f(x)的周期是2,根据函数与方程之间的关系,转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答  解:由f(x+2)=f(x),得函数f(x)的周期是2,
解:由f(x+2)=f(x),得函数f(x)的周期是2,
由h(x)=f(x)-g(x)=0得 f(x)=g(x),
分别作出函数f(x),g(x)在区间[-5,5]上的图象如图:
由图象知两个函数在区间[-5,5]内的交点个数为8个,
即函数h(x)=f(x)-g(x)在区间[-5,5]内零点的个数是8个,
故选:A
点评 本题主要考查函数零点个数的判断,根据函数与方程之间的关系,转化为两个函数的交点个数,结合数形结合是解决本题的关键.

练习册系列答案
相关题目
7.若a+2b=1(ab≠0),下列结论中错误的是( )
| A. | ab的最大值为$\frac{1}{8}$ | B. | $\frac{1}{ab}$的最小值为8 | ||
| C. | a2+ab+b2的最小值为$\frac{1}{4}$ | D. | $\frac{1}{{{a^2}+ab+{b^2}}}$的最大值为4 |
8.已知函数f(x)=ax3+x+1的图象在点(1,f(1))的处的切线过点(2,11),则 a=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2 |
6.判断:“如果一个事件是随机事件,则它发生的概率P的取值范围是(0,1)”的真假是( )
| A. | 假命题 | B. | 真命题 | C. | 不是命题 | D. | 可真可假 |
 已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.
已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.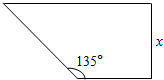 某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).