题目内容
14.已知$tanα=\frac{1}{3}$,则$\frac{{{{cos}^2}α-2{{sin}^2}α}}{{{{cos}^2}α}}$=( )| A. | $\frac{7}{9}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵已知$tanα=\frac{1}{3}$,则$\frac{{{{cos}^2}α-2{{sin}^2}α}}{{{{cos}^2}α}}$=1-2tan2α=1-$\frac{2}{9}$=$\frac{7}{9}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
6.如图,Rt△A′O′B′的直观图,且△A′O′B′为面积为1,则△AOB中最长的边长为( )


| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 1 | D. | 2 |
4.若函数f(x)=$\left\{\begin{array}{l}{f(x-4)}\\{{{2}^{x}+∫}_{0}^{\frac{π}{6}}cos3tdt,x≤0}\end{array}\right.$,则f(2016)=( )
| A. | 1 | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{5}{3}$ |
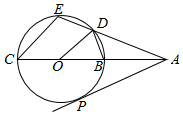 如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,