题目内容
9.已知等差数列{an}的前n项和为Sn,且a2=5,S15=150.(1)求数列{an}的通项公式;
(2)记${b_n}=\frac{1}{4}•{2^{a_n}}$,{bn}的前n项和为Tn,求Tn.
分析 (1)设等差数列{an}的首项为a1,公差为d,利用等差数列的通项公式即可得出;
(2)易知:${b_n}=\frac{1}{4}•{2^{n+2}}={2^n}$,再利用等比数列的前n项和公式即可得出.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
则a2=a1+2d=5,S15=15a1+15×7d=150,
解得a1=3,d=1,∴an=n+2.
(2)易知:${b_n}=\frac{1}{4}•{2^{n+2}}={2^n}$,
∴Tn=b1+b2+…+bn=21+22+…+2n=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.在年级举行的巴蜀中学“群英杯”辩论赛中,甲、乙、丙、丁4个班级晋级半决赛,现用抽签法将四个班级分成2个小组,则甲乙在同一组的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
4.在△ABC中,D为AB的中点,设$\overrightarrow{CA}=\overrightarrow a,\overrightarrow{CB}=\overrightarrow b$,则$\overrightarrow{CD}$=( )
| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{2}(\overrightarrow a-\overrightarrow b)$ | C. | $\overrightarrow a+\overrightarrow b$ | D. | $\overrightarrow a-\overrightarrow b$ |
14.已知$tanα=\frac{1}{3}$,则$\frac{{{{cos}^2}α-2{{sin}^2}α}}{{{{cos}^2}α}}$=( )
| A. | $\frac{7}{9}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
1.南沙群岛自古以来都是中国领土,南沙海域有A、B两个岛礁相距100海里,从A岛礁望C岛礁和B岛礁成60°的视角,从B岛礁望C岛礁和A岛礁成75°的视角,我国兰州号军舰航在A岛礁处时候B岛礁处指挥部的命令,前往C岛礁处驱赶某国入侵军舰,则我军舰此时离C岛礁距离是( )
| A. | 100($\sqrt{3}$+1)海里 | B. | 50($\sqrt{3}+1$)海里 | C. | 50$\sqrt{3}$海里 | D. | 50$\sqrt{6}$海里 |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点分别为F1,F2,一条垂直于x轴的直线交双曲线的右支于M,N两点,且MF1⊥MF2,△F1MN为等边三角形,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | 1+$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}-1$ |
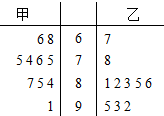 某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.
某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.