题目内容
12.已知{an}是公差不为0的等差数列,a1=1,且a1,a3,a9成等比数列.(1)求数列{an}的通项公式;
(2)若bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,求证:数列{bn}的前n项和Sn<1.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 (1)解:设等差数列{an}的公差为d≠0,∵a1,a3,a9成等比数列.
∴${a}_{3}^{2}={a}_{1}•{a}_{9}$,即(1+2d)2=1×(1+8d),化为:d2=d,d≠0,解得d=1.
∴an=1+(n-1)=n.
(2)证明:bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴Sn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$<1.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.已知x,y满足$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$,z=2x+y的最大值为m,若正数a,b满足a+b=m,则$\frac{1}{a}+\frac{4}{b}$的最小值为( )
| A. | 9 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
3.已知函数 $f(x)={2^x}-\sqrt{x}-14$,若在区间(0,16)内随机取一个数x0,则f(x0)>0的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
17.已知函数f(x)的定义域为[-1,5],在同一坐标系下,函数y=f(x)的图象与直线x=1的交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个或者2个 |
4.已知函数y=f(x)的图象关于直线x=1对称,当x<1时,f(x)=|($\frac{1}{2}$)x-1|,那么当x>1时,函数f(x)的递增区间是( )
| A. | (-∞,0) | B. | (1,2) | C. | (2,+∞) | D. | (2,5) |
1.在△ABC中,a、b、c分别为角A、B、C所对的边,且a=2,b=$\sqrt{6}$,B=$\frac{π}{3}$,则角A等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
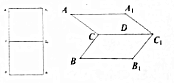 已知:矩形AA1B1B,且AB=2AA1=2,C1,C分别是A1B1、AB的中点,D为C1C中点,将矩形AA1B1B沿着直线C1C折成一个60°的二面角,如图所示.
已知:矩形AA1B1B,且AB=2AA1=2,C1,C分别是A1B1、AB的中点,D为C1C中点,将矩形AA1B1B沿着直线C1C折成一个60°的二面角,如图所示.