题目内容
4.已知函数y=f(x)的图象关于直线x=1对称,当x<1时,f(x)=|($\frac{1}{2}$)x-1|,那么当x>1时,函数f(x)的递增区间是( )| A. | (-∞,0) | B. | (1,2) | C. | (2,+∞) | D. | (2,5) |
分析 由题意可得可将x换为2-x,可得x>1的f(x)的解析式,画出图象,即可得到所求递增区间.
解答  解:函数y=f(x)的图象关于直线x=1对称,
解:函数y=f(x)的图象关于直线x=1对称,
当x<1时,f(x)=|($\frac{1}{2}$)x-1|,
可得x>1时,f(x)=|($\frac{1}{2}$)2-x-1|,即为f(x)=|2x-2-1|,
画出x>1时,y=f(x)的图象,
可得递增区间为(2,+∞).
故选:C.
点评 本题考查函数的对称性和单调性,考查数形结合的思想方法,运用对称求得x>1的解析式是解题的关键,属于中档题.

练习册系列答案
相关题目
15.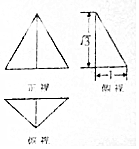 已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
 已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
19.已知直线l1:(m-2)x-y+5=0与l2:(m-2)x+(3-m)y+2=0平行,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | 4 |
14.“a≤0”是“函数f(x)=ax+lnx存在极值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |