题目内容
已知双曲线中心在原点,以坐标轴为对称轴,且与圆x2+y2=17相交于A(4,-1),若圆在A点处的切线与双曲线的渐近线平行,求此双曲线方程.
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求圆的切线方程,进而得到双曲线的渐近线方程,再用待定系数法求双曲线的方程.
解答:
解:圆在A点的切线l可设为y=k(x-4)-1.
由题可得
=
,解得k=4,
因为l与双曲线的一条渐近线平行,双由曲线的定义可知,
=4(1),
而点A(4,-1)在双曲线上,代入可得
-
=1(2).
联立方程组(1),(2),可以算出a2=
,b2=255,
所以所求双曲线方程为16x2-y2=255.
由题可得
| |-4k-1| | ||
|
| 17 |
因为l与双曲线的一条渐近线平行,双由曲线的定义可知,
| b |
| a |
而点A(4,-1)在双曲线上,代入可得
| 16 |
| a2 |
| 1 |
| b2 |
联立方程组(1),(2),可以算出a2=
| 255 |
| 16 |
所以所求双曲线方程为16x2-y2=255.
点评:本题考查圆的切线方程,考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的体积是( )
A、20
| ||||
B、
| ||||
C、
| ||||
| D、50π |
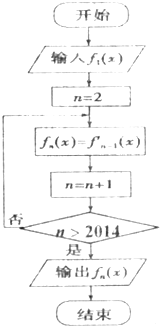 在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)等于函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )
在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)等于函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
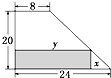 (函数的应用)某厂有许多形状为直角梯形的铁皮边角料(如图),为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图阴影部分)备用,则截取的矩形面积的最大值为
(函数的应用)某厂有许多形状为直角梯形的铁皮边角料(如图),为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图阴影部分)备用,则截取的矩形面积的最大值为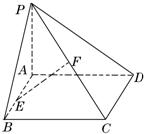 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.