题目内容
已知数列{an}为等比数列,其前n项和为Sn,已知a3+a5=-
,且对于任意的n∈N,有S1,S3,S2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),求Tn=
+
+
+…+
.
| 5 |
| 32 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),求Tn=
|
|
|
|
考点:数列的求和,等比数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)由已知得
,由此求出首项和公比,从而能求出an=(-
)n.
(Ⅱ)由bn=n,得|
|=
,由此利用错位相减法能求出Tn.
|
| 1 |
| 2 |
(Ⅱ)由bn=n,得|
| bn |
| an |
| n |
| 2n |
解答:
解:(Ⅰ)由已知得
,
解得a1=-
,q=-
,
∴an=(-
)n.
(Ⅱ)∵bn=n,∴|
|=
,
∵Tn=
+
+
+…+
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②,得:
Tn=
+
+
+…+
-
=
-
=1-
-
,
∴Tn=2-
.
|
解得a1=-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=(-
| 1 |
| 2 |
(Ⅱ)∵bn=n,∴|
| bn |
| an |
| n |
| 2n |
∵Tn=
|
|
|
|
∴Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
①-②,得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| ||||
1-
|
| n |
| 2n+1 |
=1-
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| n+2 |
| 2n |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
与函数y=x为相同函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=elnx | ||
| D、y=log22x |
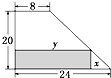 (函数的应用)某厂有许多形状为直角梯形的铁皮边角料(如图),为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图阴影部分)备用,则截取的矩形面积的最大值为
(函数的应用)某厂有许多形状为直角梯形的铁皮边角料(如图),为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图阴影部分)备用,则截取的矩形面积的最大值为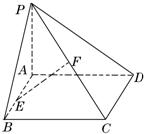 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.