题目内容
2.已知复数z1=1+i,z2=3-2i,z3=z2-z1,z4=z1•z2.(Ⅰ)z3,z4;
(Ⅱ)在复平面上,复数z3,z4所对应的点分别为A,B,求|AB|.
分析 (I)利用复数的运算法则即可得出.
(II)利用数形结合、两点之间的距离公式即可得出.
解答 解:(Ⅰ)z3=(3-2i)-(1+i)=2-3i,z4=(1+i)•(3-2i)=5+i.
(Ⅱ)依题意知A(2,-3),B(5,1),
∴$|AB|=\sqrt{{{(5-2)}^2}+{{[{1-(-3)}]}^2}}=5$.
点评 本题考查了复数的运算法则、数形结合、两点之间的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.若△ABC内角A、B、C所对的边分别为a、b、c,且${a^2}={c^2}-{b^2}+\sqrt{3}ba$,则∠C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{4}$ |
7.若f(x)=x4-3x3+1,则f′(x)=( )
| A. | 4x3-6x2 | B. | 4x3-9x2 | C. | 4x3+6x2 | D. | 4x3-6x2+1 |
11.曲线y=$\frac{1}{3}{x^3}$+x-$\frac{1}{3}$在点(1,1)处的切线与坐标轴围成的三角形面积为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
12.y=4cosx-e|x|图象可能是( )
| A. | 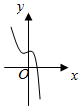 | B. | 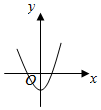 | C. | 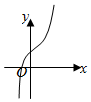 | D. | 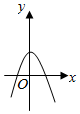 |