题目内容
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若m+k=0,直线A1M与NA2的斜率分别为k1,k2.试问:是否存在实数λ,使得k1+λk2=0?若存在,求λ的值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用已知条件求出a=3,通过离心率求出c,然后求出b,即可得到椭圆的方程.
(Ⅱ)解法一:由m+k=0,直线l:y=kx-k,直线恒过定点D(1,0),设直线A1M的方程为y=k1(x+3),直线NA2的方程为y=k2(x-3).qc M,N的坐标,由M,D,N三点共线,推出k2=2k1,得到k1+(-
)k2=0,然后判断存在λ=-
使得使得k1+λk2=0.
解法二:由m+k=0知,m=-k,直线l过定点D(1,0),当直线l的倾斜角α→∞时,M→(1,
),N→(1,-
),推出k1→
,k2→
,λ→
=-
,猜想:存在λ=-
满足条件,下面证明猜想正确 联立方程组
,设M(x1,y1),N(x2,y2),通过韦达定理求出k1,k2,然后验证是否存在实数λ,使得k1+λk2=0.
(Ⅱ)解法一:由m+k=0,直线l:y=kx-k,直线恒过定点D(1,0),设直线A1M的方程为y=k1(x+3),直线NA2的方程为y=k2(x-3).qc M,N的坐标,由M,D,N三点共线,推出k2=2k1,得到k1+(-
| 1 |
| 2 |
| 1 |
| 2 |
解法二:由m+k=0知,m=-k,直线l过定点D(1,0),当直线l的倾斜角α→∞时,M→(1,
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
| -k1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
解答:
(本小题满分13分)
解:(Ⅰ)由题设可知a=3
因为e=
即
=
,所以c=2
.又因为b2=a2-c2=9-8=1
所以椭圆C的方程为:
+y2=1…(4分)
(Ⅱ)解法一:
由m+k=0知:直线恒过定点D(1,0),…(5分)
设直线A1M的方程为y=k1(x+3),直线NA2的方程为y=k2(x-3).
联立方程组
,消去y得:(1+9k12)x2+54k1x+81k12-9=0
解得点M的坐标为M(
,
). …(8分)
同理,可解得点N的坐标为N(
,
)…(9分)
由M,D,N三点共线,有
=
,…(10分)
化简得(k2-2k1)(18k1k2+2)=0.
由题设可知k1与k2同号,所以k2=2k1,即.k1+(-
)k2=0…(12分)
所以,存在λ=-
使得使得k1+λk2=0.…(13分)
解法二:
由m+k=0知,m=-k,
直线l方程化为y=k(x-1),所以l过定点D(1,0)…(5分)
当直线l的倾斜角α→∞时,M→(1,
),N→(1,-
)
此时k1→
,k2→
,λ→
=-
由此可猜想:存在λ=-
满足条件,下面证明猜想正确 …(7分)
联立方程组
⇒(1+9k2)x2-18k2x+9k2-9=0,
设M(x1,y1),N(x2,y2),
则x1+x2=
,x1•x2=
…(10分)
∵k1=
,k2=
所以λ=-
时,k1+λk2=
-
=
=
=
=0…(12分)
由此可得猜想正确,因此,存在λ=-
使得k1+λk2=0成立 …(13分)
解:(Ⅰ)由题设可知a=3
因为e=
2
| ||
| 3 |
| c |
| a |
2
| ||
| 3 |
| 2 |
所以椭圆C的方程为:
| x2 |
| 9 |
(Ⅱ)解法一:
由m+k=0知:直线恒过定点D(1,0),…(5分)
设直线A1M的方程为y=k1(x+3),直线NA2的方程为y=k2(x-3).
联立方程组
|
解得点M的坐标为M(
| 3-27k12 |
| 1+9k12 |
| 6k1 |
| 1+9k12 |
同理,可解得点N的坐标为N(
| 27k22-3 |
| 1+9k22 |
| -6k2 |
| 1+9k22 |
由M,D,N三点共线,有
| ||
|
-
| ||
|
化简得(k2-2k1)(18k1k2+2)=0.
由题设可知k1与k2同号,所以k2=2k1,即.k1+(-
| 1 |
| 2 |
所以,存在λ=-
| 1 |
| 2 |
解法二:
由m+k=0知,m=-k,
直线l方程化为y=k(x-1),所以l过定点D(1,0)…(5分)
当直线l的倾斜角α→∞时,M→(1,
2
| ||
| 3 |
2
| ||
| 3 |
此时k1→
| ||
| 6 |
| ||
| 3 |
| -k1 |
| k2 |
| 1 |
| 2 |
由此可猜想:存在λ=-
| 1 |
| 2 |
联立方程组
|
设M(x1,y1),N(x2,y2),
则x1+x2=
| 18k2 |
| 1+9k2 |
| 9k2-9 |
| 1+9k2 |
∵k1=
| y1 |
| x1+3 |
| y2 |
| x2-3 |
所以λ=-
| 1 |
| 2 |
| y1 |
| x1+3 |
| 1 |
| 2 |
| y2 |
| x2-3 |
=
| 2k(x1-1)(x2-3)-k(x2-1)(x1+3) |
| 2(x1+3)(x2-3) |
| k(x1x2-5x2-5x1+9) |
| 2(x1+3)(x2-3) |
k(
| ||||
| 2(x1+3)(x2-3) |
=
| k(9k2-9-90k2+9+81k2) |
| 2(1+9k2)(x1+3)(x2-3) |
由此可得猜想正确,因此,存在λ=-
| 1 |
| 2 |
点评:本题考查直线与椭圆方程的综合应用,考查存在性问题的处理方法,椭圆方程的求法,韦达定理的应用,三点共线的充要条件,注意方法二中,极限思想的应用,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求:A,B两个节目至少有一个选中,且A,B同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为( )
| A、1860 | B、1320 |
| C、1140 | D、1020 |
在等比数例{an}中,2a4,a6,48成等差数列,且a3•a5=64,则{an}的前8项和为( )
| A、255 | B、85 |
| C、255或-85 | D、255或85 |
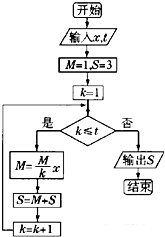 执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )
执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,AB=4,∠ABC=30°,D是边BC上的一点,且
•
=
•
,则
•
的值为( )
| AD |
| AB |
| AD |
| AC |
| AD |
| AB |
| A、0 | B、4 | C、8 | D、-4 |