题目内容
1．设a，b∈R，定义：M（a，b）=$\frac{a+b+|a-b|}{2}$，m（a，b）=$\frac{a+b-|a-b|}{2}$．下列式子错误的是（ ）| A． | M（a，b）+m（a，b）=a+b | B． | m（|a+b|，|a-b|）=|a|-|b| | C． | M（|a+b|，|a-b|）=|a|+|b| | D． | m（M（a，b），m（a，b））=m（a，b） |
分析 依据新定义进行列式计算，逐个验证选项即可．
解答 解：由定义可知M（a，b）+m（a，b）=$\frac{a+b+|a-b|}{2}$+$\frac{a+b-|a-b|}{2}$=a+b，故A正确．
m（|a+b|，|a-b|）=|a|-|b|=$\frac{|a+b|+|a-b|-||a+b|-|a-b||}{2}$，
∴当|a+b|≥|a-b|时，m（|a+b|，|a-b|）=|a-b|，
当|a+b|＜|a-b|时，m（|a+b|，|a-b|）=|a+b|，故B错误．
故选B．
点评 本题考查了对新定义的理解与应用，属于基础题．
练习册系列答案
相关题目
16．若实数x，y满足$\sqrt{{x}^{2}+（y-13）^{2}}$-$\sqrt{{x}^{2}+（y+13）^{2}}$=10，则动点P（x，y）的轨迹方程是（ ）
| A． | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1（x＞0） | B． | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1（x＜0） | ||
| C． | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1（y＞0） | D． | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1（y＜0） |
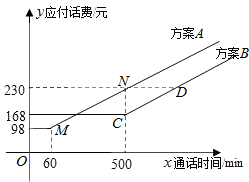电信局为了配合客户不同需要，设有A，B两种优惠方案．这两种方案应付话费（元）与通话时间x（min）之间的关系如图所示，其中D的坐标为（$\frac{2120}{3}$，230）．