题目内容
6.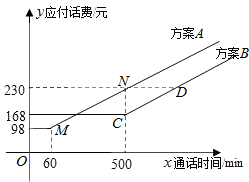 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230).
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230).(1)若通话时间为2小时,按方案A,B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B比方案A优惠?
分析 (1)设这两种方案的应付话费与通话时间的函数关系为fA(x)和fB(x),由图知M(60,98),N(500,230),C(500,168),MN∥C,分别求出fA(x)和fB(x),由此能求出通话时间为2小时,按方案A,B各付话费多少元.
(2)求出fB(n+1)-fB(n),n>500,由此能求出方案B从500分钟以后,每分钟收费多少元.
(3)由图知,当0≤x≤60时,fA(x)fB(x).由此能求出通话时间在什么范围内,方案B比方案A优惠.
解答 解:(1)设这两种方案的应付话费与通话时间的函数关系为fA(x)和fB(x),
由图知M(60,98),N(500,230),C(500,168),MN∥C,
则${f}_{A}(x)=\left\{\begin{array}{l}{98,0≤x≤60}\\{\frac{3}{10}x+80,x>60}\end{array}\right.$,
${f}_{B}(x)=\left\{\begin{array}{l}{168,0≤x≤50}\\{\frac{3}{10}x+18,x>500}\end{array}\right.$.
∴通话2小时,方案A应付话费:${f}_{A}(120)=\frac{3}{10}×120+80=116$元,
方案B应付话费:168元.
(2)∵${f}_{B}(n+1)-{f}_{B}(n)=\frac{3}{10}(n+1)+18$-($\frac{3}{10}n+18$)=0.3,n>500,
∴方案B从500分钟以后,每分钟收费0.3元.
(3)由图知,当0≤x≤60时,fA(x)<fB(x),
当60<x≤500时,由fA(x)>fB(x),得$\frac{3}{10}x+80>168$,
解得x>$\frac{880}{3}$,∴$\frac{880}{3}<x≤500$,
当x>500时,fA(x)>fB(x).
综上,通话时间在($\frac{880}{3}$,+∞)内,方案B比方案A优惠.
点评 本题考查函数知识在生产生活中的实际应用,是中档题,解题时要认真审题,注意分段函数的性质的合理运用.

| A. | M(a,b)+m(a,b)=a+b | B. | m(|a+b|,|a-b|)=|a|-|b| | C. | M(|a+b|,|a-b|)=|a|+|b| | D. | m(M(a,b),m(a,b))=m(a,b) |
| A. | $\frac{15}{4}$ | B. | 3 | C. | 2 | D. | -1 |

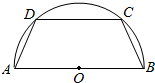 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.