题目内容
已知向量
,
满足(
+2
)•(
-
)=-6,且|
|=1,|
|=2,则
在
上的投影为 .
| a |
| b |
. |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量数量积的运算化简已知的是,利用条件和向量的投影的含义可得:|
|cosθ=
,即可得到答案.
| a |
| 1 |
| 2 |
解答:
解:由题意得,(
+2
)•(
-
)=-6,则
2-2
2+
•
=-6,
因为|
|=1,|
|=2,设两个向量
,
的夹角是θ,
所以|
||
|cosθ=1,则|
|cosθ=
,即
在
上投影为
,
故答案为:
.
. |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
因为|
| a |
| b |
| a |
| b |
所以|
| a |
| b |
| a |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查向量数量积的运算,以及向量的投影的含义,解题的关键是抓住向量的投影的含义,结合已知条件化简.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
函数y=x•e-x在x∈[2,4]上的最小值为( )
| A、0 | ||
B、
| ||
C、
| ||
D、
|
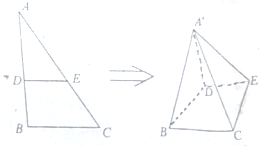 如图,在直角△ABC中,B=90°,BC=1,AB=
如图,在直角△ABC中,B=90°,BC=1,AB=