Question

20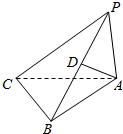．如图所示的三棱锥P-ABC中，D是棱PB的中点，已知PA=BC=2，AB=4，CB⊥AB，PA⊥平面ABC，则异面直线PC，AD所成角的余弦值为$\frac{\sqrt{30}}{10}$．

Answer 1

分析 以B为原点，BC为x轴，BA为y轴，过B平行于AP的直线为z轴，建立空间直角坐标系，利用向量法能求出异面直线PC，AD所成角的余弦值．

解答 解：∵三棱锥P-ABC中，PA⊥平面ABC，D是棱PB的中点，PA=BC=2，AB=4，CB⊥AB，
∴以B为原点，BC为x轴，BA为y轴，过B平行于AP的直线为z轴，建立空间直角坐标系，
P（0，4，2），C（2，0，0），
A（0，4，0），B（0，0，0），D（0，2，1），
$\overrightarrow{PC}$=（2，-4，-2），$\overrightarrow{AD}$=（0，-2，1），
设异面直线PC，AD所成角为θ，
则cosθ=$\frac{|\overrightarrow{PC}•\overrightarrow{AD}|}{|\overrightarrow{PC}|•|\overrightarrow{AD}|}$=$\frac{|6|}{\sqrt{24}×\sqrt{5}}$=$\frac{\sqrt{30}}{10}$．
∴异面直线PC，AD所成角的余弦值为$\frac{\sqrt{30}}{10}$．
故答案为：$\frac{\sqrt{30}}{10}$．

点评 本题考查异面直线所成角的余弦值的求法，是基础题，解题时要认真审题，注意向量法的合理运用．