题目内容
10.若sinθ=-$\frac{3}{5}$,θ∈(-$\frac{π}{2}$,0),则2sin(2θ+$\frac{π}{3}$)=$\frac{7\sqrt{3}-24}{25}$.分析 由条件利用同角三角函数的基本关系求得cosθ,利用二倍角公式求得sin2θ和cos2θ,再利用两角和的正弦公式求得2sin(2θ+$\frac{π}{3}$)的值.
解答 解:∵sinθ=-$\frac{3}{5}$,θ∈(-$\frac{π}{2}$,0),∴cosθ=$\sqrt{{1-sin}^{2}θ}$=$\frac{4}{5}$,
∴sin2θ=2sinθcosθ=2•(-$\frac{3}{5}$)•$\frac{4}{5}$=-$\frac{24}{25}$,cos2θ=2cos2θ-1=$\frac{7}{25}$,
则2sin(2θ+$\frac{π}{3}$)=2sin2θcos$\frac{π}{3}$+2cos2θsin$\frac{π}{3}$=2•(-$\frac{24}{25}$)•$\frac{1}{2}$+2•$\frac{7}{25}$•$\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}-24}{25}$,
故答案为:$\frac{7\sqrt{3}-24}{25}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式的应用,两角和的正弦公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列函数中,既是偶函数又在区间(0,+∞)内是单调减函数的是( )
| A. | y=log0.5|x| | B. | y=${3}^{{x}^{2}}$ | C. | y=-x2+x | D. | y=cosx |
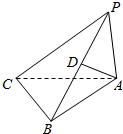 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$. 已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.
已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.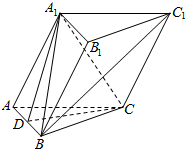 在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.