题目内容
8. 有一机械传输装置(如图)将动轮⊙O的直径为2m,已知OA=2cm,OB=3cm,M、N是切点,OA∥BN,求物品从A点传输到B点的路程.
有一机械传输装置(如图)将动轮⊙O的直径为2m,已知OA=2cm,OB=3cm,M、N是切点,OA∥BN,求物品从A点传输到B点的路程.
分析 连接OM,ON,则OM⊥AM,ON⊥BN,求出AM,BN,$\widehat{MN}$,即可求物品从A点传输到B点的路程.
解答 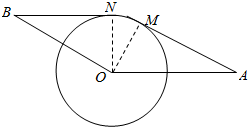 解:连接OM,ON,则OM⊥AM,ON⊥BN,
解:连接OM,ON,则OM⊥AM,ON⊥BN,
∴AM=$\sqrt{4-1}$=$\sqrt{3}$,BN=$\sqrt{9-1}$=2$\sqrt{2}$,∠AOM=60°,
∵OA∥BN,
∴∠MON=30°=$\frac{π}{6}$,
∴$\widehat{MN}$=$\frac{π}{6}$,
∴物品从A点传输到B点的路程为$\sqrt{3}$+2$\sqrt{2}$+$\frac{π}{6}$.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
18.把函数y=2sin(2x+$\frac{π}{6}$)的图象经过变换,得到y=-2sin2x的图象,这个变换是( )
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位. |
16.若可导函数f(x)满足f′(3)=9,则f(3x2)在x=1处的导数值为( )
| A. | 1 | B. | 9 | C. | 27 | D. | 54 |
3.下列函数中,y的最小值是4的是( )
| A. | y=2x$+\frac{2}{x}$ | B. | y=2x+4•2-x | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=$\frac{4}{sinx}+sinx(0<x<4)$ |
17.已知数列{an}满足:a1=2,an+1=-2an(n∈N*).若从数列{an}的前10项中随机抽取一项,则该项不小于8的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
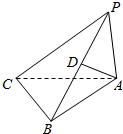 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$. 已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.
已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.