题目内容
15.已知A(a,0),B(0,b),C(cosα,sinα)三点共线,其中a>0,b>0,α∈(0,$\frac{π}{2}$),则$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$的最小值$\frac{2}{\sqrt{{a}^{2}{+b}^{2}}}$.分析 先求出ab=asinα+bcosα,利用基本不等式的性质判断即可.
解答 解:∵A(a,0),B(0,b),C(cosα,sinα)三点共线,
∴-$\frac{b}{a}$=$\frac{sinα-b}{cosα}$,即ab=asinα+bcosα,
又a>0,b>0,α∈(0,$\frac{π}{2}$),
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥2$\sqrt{\frac{1}{{a}^{2}}•\frac{1}{{b}^{2}}}$=$\frac{2}{ab}$=$\frac{2}{\sqrt{{a}^{2}{+b}^{2}}sin(α+θ)}$≥$\frac{2}{\sqrt{{a}^{2}{+b}^{2}}}$,
(θ=arccos$\frac{a}{\sqrt{{a}^{2}{+b}^{2}}}$),当且仅当a=b时“=”成立,
故答案为:$\frac{2}{\sqrt{{a}^{2}{+b}^{2}}}$.
点评 本题考察了斜率问题,考察基本不等式的性质,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.求值:cos$\frac{π}{5}$cos$\frac{2π}{5}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
3.下列函数中,y的最小值是4的是( )
| A. | y=2x$+\frac{2}{x}$ | B. | y=2x+4•2-x | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=$\frac{4}{sinx}+sinx(0<x<4)$ |
7.命题?x∈R,cosx≤1的真假判断及其否定是( )
| A. | 真,?x0∈R,cosx0>1 | B. | 真,?x∈R,cosx>1 | ||
| C. | 假,?x0∈R,cosx0>1 | D. | 假,?x∈R,cosx>1 |
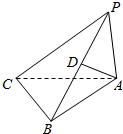 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.