题目内容
9.已知函数f(x)=x2-mx-m+3,试判断是否存在实数m满足一个零点在(0,1)内,另一个零点在(1,2)内?若存在,求出m的取值范围;若不存在,请说明理由.分析 根据一元二次函数根的分布建立不等式关系进行求解即可.
解答 解:若存在实数m满足一个零点在(0,1)内,另一个零点在(1,2),
则满足$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$.即$\left\{\begin{array}{l}{3-m>0}\\{4-2m<0}\\{7-3m>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<3}\\{m>2}\\{m<\frac{7}{3}}\end{array}\right.$,得2<m<3,
即存在2<m<3时函数f(x)满足一个零点在(0,1)内,另一个零点在(1,2)内.
点评 本题主要考查函数零点与根的关系,利用一元二次方程根的分布是解决本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
17.已知数列{an}满足:a1=2,an+1=-2an(n∈N*).若从数列{an}的前10项中随机抽取一项,则该项不小于8的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
14.若函数y=(a2-1)x在R上是减函数,则有( )
| A. | |a|<1 | B. | 1<|a|<2 | C. | 1<|a|<$\sqrt{2}$ | D. | |a|>$\sqrt{2}$ |
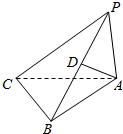 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$. 已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.
已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.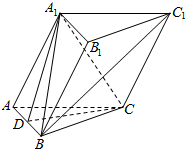 在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.