题目内容
12.已知函数f(x)=ax+2经过点(1,4),则不等式f(x+2)≥3f(-x)的解集为( )| A. | [log2$\frac{3}{2}$,+∞) | B. | (-∞,log2$\frac{3}{2}$) | C. | [log25,+∞) | D. | (-∞,log25] |
分析 将(1,4)代入f(x)求出a的值,得到f(x)的解析式,然后利用换元法解出不等式.
解答 解:∵f(1)=a+2=4,∴a=2,∴f(x)=2x+2.
∵f(x+2)≥3f(-x),即2x+2+2≥3(2-x+2),∴4•2x+2≥$\frac{3}{{2}^{x}}$+6.
令2x=t(t>0),则4t2-4t-3≥0.解得t≥$\frac{3}{2}$.即2x≥$\frac{3}{2}$,∴x≥log2$\frac{3}{2}$.
故选A.
点评 本题考查了指数不等式的解法,换元思想,属于中档题.

练习册系列答案
相关题目
3.下列函数中,y的最小值是4的是( )
| A. | y=2x$+\frac{2}{x}$ | B. | y=2x+4•2-x | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=$\frac{4}{sinx}+sinx(0<x<4)$ |
7.命题?x∈R,cosx≤1的真假判断及其否定是( )
| A. | 真,?x0∈R,cosx0>1 | B. | 真,?x∈R,cosx>1 | ||
| C. | 假,?x0∈R,cosx0>1 | D. | 假,?x∈R,cosx>1 |
17.已知数列{an}满足:a1=2,an+1=-2an(n∈N*).若从数列{an}的前10项中随机抽取一项,则该项不小于8的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
2.下列函数中,既是偶函数又在区间(0,+∞)内是单调减函数的是( )
| A. | y=log0.5|x| | B. | y=${3}^{{x}^{2}}$ | C. | y=-x2+x | D. | y=cosx |
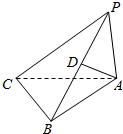 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.