题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}x+\frac{2}{e},x<0\\ \frac{x}{e^x},x≥0\end{array}$,若f(x1)=f(x2)=f(x3)(x1<x2<x3),则$\frac{{f({x_2})}}{x_1}$的取值范围是( )| A. | (-1,0) | B. | (-2,-1) | C. | (-∞,0) | D. | (1,+∞) |
分析 利用导数法,分析函数的单调性及极值,可得f(x1)=f(x2)=f(x3)∈(0,$\frac{1}{e}$),进而可得:-$\frac{2}{e}$<x1<-$\frac{1}{e}$,故$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$=1+$\frac{\frac{2}{e}}{{x}_{1}}$∈(-1,0).
解答 解:函数f(x)=$\left\{\begin{array}{l}x+\frac{2}{e},x<0\\ \frac{x}{e^x},x≥0\end{array}$,
∴函数f′(x)=$\left\{\begin{array}{l}1,x<0\\ \frac{1-x}{{e}^{x}},x≥0\end{array}\right.$,
故当x<0时,函数为增函数,且f(x)<$\frac{2}{e}$,
当0≤x<1时,函数为增函数,且0≤f(x)<$\frac{1}{e}$,
当x≥1时,函数为减函数,且0<f(x)≤$\frac{1}{e}$,
若f(x1)=f(x2)=f(x3)(x1<x2<x3),
则f(x1)=f(x2)=f(x3)∈(0,$\frac{1}{e}$),
即-$\frac{2}{e}$<x1<-$\frac{1}{e}$,
故$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$=1+$\frac{\frac{2}{e}}{{x}_{1}}$∈(-1,0),
故选:A
点评 本题考查的知识点是分段函数的应用,利用导数法研究函数的单调性,利用导数法研究函数的极值,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.春节期间和谐小区从初一至初八连续8天举办大型文艺汇演,居民甲随机选择其中的连续3天观看演出,那么他在初一至初四期间连续3天看演出的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
16.在拍毕业照时,六个同学排成一排照相,要求其中一对好友甲和乙相邻,且同学丙不能和甲相邻的概率为( )
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
3.执行如下图所示的程序框图,输出S的值为( )


| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
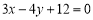 与坐标轴的交点是圆
与坐标轴的交点是圆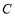 一条直径的两端点.
一条直径的两端点.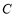 的方程;
的方程;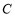 的弦
的弦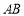 长度为
长度为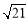 且过点
且过点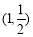 ,求弦
,求弦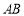 所在直线的方程.
所在直线的方程. ,则
,则 ”的否命题是( )
”的否命题是( )
 ,则
,则
 ,则
,则